基礎知識

パソコンの引き算 - なぜ補数を取るとマイナス表現になるのか
とっても古い『栢木先生の基本情報技術者教室』を読んでいて、負数の表現がさっぱり分かりませんでした。
それぞれのビットを反転させ、1を加えることによって「2の補数」を作れば負数が出来上がるというのは説明がありますが、では、そうすることによって、なぜマイナスが足し算で可能になるのでしょうか。
この説明ではさっぱりわかりません。
この説明は、令和2年度版でも同じようなものです。
毎年改定がある人気書なのに、初学者には分かりにくいこのようなところは、なんで何年も前から説明が全く変わらないのでしょうかね。
新しい知識の部分だけが少しばかり書き換えられて、基礎知識の説明は、一向に昔のまんま。
逆に言えば、これだから、基本部分の作りがしっかりしている栢木先生の本は、数年前の古本でも、概要をつかむくらいなら、結構遜色なく使えるのです。
毎年改定がある人気書なのに、初学者には分かりにくいこのようなところは、なんで何年も前から説明が全く変わらないのでしょうかね。
新しい知識の部分だけが少しばかり書き換えられて、基礎知識の説明は、一向に昔のまんま。
逆に言えば、これだから、基本部分の作りがしっかりしている栢木先生の本は、数年前の古本でも、概要をつかむくらいなら、結構遜色なく使えるのです。
説明通り丸暗記をすれば、その場は計算できるかもしれませんが、感覚的にすっきり納得がいっていないと、そんな記憶が長続きして役に立つはずがありません。
ある数と、補数を足し合わせると 0 になる
「2の補数」とは、元の数と足し合わせて、与えられた数の最大値より1大きくなる数なので、元の数と足し合わせると、桁上がりします。
例えば8ビットなら、9ビット目が1になり、8ビット目以降はすべて0になります。パソコンは、指示されたこと以外はしませんから、8ビット目までの演算が指定されていれば、9ビット目がいくら桁上がりしていても、8ビット目までしか感知しません。9ビット目は無視されます。
ということは、「1+(-1)=0」と、一つの数と、その数のマイナス表現である補数を足し合わせると、必ず 0 になります。
足し合わせて 0 になるということは、同じ数のマイナスが表現できたということです。
そして、下の表を見ると、どの段階でも、一つ下に下がれば、1ずつ数値が下がっていくのが分かります。すなわち -128 から +127 までの範囲でだけなら、これでうまくマイナスの計算ができたということです。
指定された範囲内でのみ、このやり方が有効になるのですから、この範囲を逸脱する答えになるときは、この足し算の結果は、当然でたらめになってしまいます。
8ビット目を見ると、プラスは 0 、マイナスなら 1 になっています。「マイナス同士を足し合わせて、8ビット目が 、「1+1」で0 になることは無いのか」という疑問が浮かんできますが、そのような場合は、計算結果が「-128 から +127 までの範囲」を逸脱しているからのようです。結果が範囲にとどまっていれば、下からの桁上がりによって、必ず8ビット目も桁上がりし、「1+1+1=1」になるようですね。
| 10進数 | 2進数 |
|---|---|
| +127 | 01111111 |
| +126 | 01111110 |
| ~ | |
| +3 | 00000011 |
| +2 | 00000010 |
| +1 | 00000001 |
| 0 | 00000000 |
| -1 | 11111111 |
| -2 | 11111110 |
| -3 | 11111101 |
| ~ | |
| -126 | 10000010 |
| -127 | 10000001 |
| -128 | 10000000 |
プラスとマイナスとで絶対値で表現できる範囲が異なる
プラスは、+127 まで、マイナスは -128 までと、表現できる絶対値の数値は異なります。
見てみると、-128 は、0 の対で、8ビット目だけが1になっているバージョンの様です。0 は正に入りますから、正は、「127から0」までで128個、負は、「-1から-128」まででこちらも128個です。
本屋で立ち読みしながら、平成23年度のと今のとで、栢木先生の本は、あまり説明部分は変わっていないようなので、改めて買い直す必要性をあまり感じていなかったのですが、令和2年度秋の試験が延期されたので、栢木先生の本を使って、素早くもう一度最近の内容を含めて、知識の整理をしたくなったので、半分「無駄かな」と思いながら、昨年度版も手に入れてみました。
両者を見比べてみて、大きな違いは、例題を最近のものに差し替えているぐらいで、説明は概ね同じでした。ビジネス用語などを中心に、若干の用語を補足するといった改定がなされているようです。
しかし、ちょっと気になるのは、23年のには入っていた、+127から-128までの上の2進数の表が、令和1年度版では消えていることです。(バイアス127の説明なども)
ページ数の都合なのでしょうが、この表は、他書には載っていないものも多くて、栢木先生の本の良いところの一つだっただけに、改定のあり方は、もう少し慎重にしてほしいものだと思います。
毎年改定している割には、新しい用語についても、あまり本気で加えていこうとしているようにも見えませんし。
両者を見比べてみて、大きな違いは、例題を最近のものに差し替えているぐらいで、説明は概ね同じでした。ビジネス用語などを中心に、若干の用語を補足するといった改定がなされているようです。
しかし、ちょっと気になるのは、23年のには入っていた、+127から-128までの上の2進数の表が、令和1年度版では消えていることです。(バイアス127の説明なども)
ページ数の都合なのでしょうが、この表は、他書には載っていないものも多くて、栢木先生の本の良いところの一つだっただけに、改定のあり方は、もう少し慎重にしてほしいものだと思います。
毎年改定している割には、新しい用語についても、あまり本気で加えていこうとしているようにも見えませんし。
固定小数点の負数
平成23年秋期 問2
10進数-5.625を,8ビット固定小数点形式による2進数で表したものはどれか。ここで,小数点位置は3ビット目と4ビット目の間とし,負数には2の補数表現を用いる。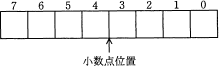
10進数-5.625を,8ビット固定小数点形式による2進数で表したものはどれか。ここで,小数点位置は3ビット目と4ビット目の間とし,負数には2の補数表現を用いる。

- 01001100
- 10100101
- 10100110
- 11010011
まず、5.625を2進数にします。
小数点がある場合は、小数点以上と以下とで、別々に2進数に直します。
5=101
0.625=0.101
これをつなげた数を、枠に当てはめて書くと
0101.1010
補数を取って(各ビットを反転させて、最後の桁に1を加える)
1010.0110
小数点がある場合は、小数点以上と以下とで、別々に2進数に直します。
5=101
0.625=0.101
これをつなげた数を、枠に当てはめて書くと
0101.1010
補数を取って(各ビットを反転させて、最後の桁に1を加える)
1010.0110
解答:3
補数にする時には、小数点以上と以下とで、別々に補数を取るのではなくて、小数点以下もつなげた数の補数を取らないといけないようです。
まあ、考えてみれば、そうしないとコンピューターは、うまく計算できないでしょうね。こうしておけば、小数点の桁の位置をずらすだけで、小数点がない場合と同じように計算を処理することができるので。
元々、「固定小数点数は、『ビット列のどの位置に小数点があるか』を暗黙的了解として扱う表現方法」(『キタミ』)ですから、コンピューターは、1011010 や 10100110 の計算をしているだけです。
本当に知識がないものには順を追って説明してくれないと
本当に知識がないものには順を追って説明してくれないと、理解できません。
小学校の教科書を見ていると、足し算を教えるのにも、
- 繰り上がりのない一桁の足し算
- 繰り上がりがある1桁の足し算
- 2桁目だけが繰り上がる2桁の足し算
- 1桁目も2桁目も繰り上がる2桁の足し算
- 3桁以上の足し算
と細かく順を追って説明してあります。
一般の人が、子ども(他人)に算数を教えることが出来ないのは、これらのことを自分はもう既に知って感覚的にやっているので、その理解の段階の違いを細かく把握できていないからです。
基本情報の教科書も、「分からない人に向けてきちんと分かるように解説してある」ものは、数ある中の一握りの様です。

